To unleash the computational power of quantum computers in applications of practical interest, the error rates of quantum logic gates need to be further reduced. In superconducting quantum computers, leakage errors to non-computational states are currently one of the dominant sources of gate errors. In our new paper, we propose and demonstrate novel control pulse shapes that can reduce the leakage error of fast single-qubit gates by an order of magnitude. Overall, the new methods enable faster quantum gates with lower errors, thus enhancing the computational capabilities of superconducting quantum computers.
As a thought experiment, imagine you are writing a piece of code to simulate the trajectory of a rocket for your physics homework assignment. However, the results you get from the simulation seem suspicious since the outcome varies randomly between different runs of the code. What is more, the results become weirder with each new line of code you add until the output looks like noise.
You spend hours debugging your code but eventually you are convinced that there is nothing wrong. Finally, you start suspecting that there must instead be something wrong with your computer hardware since you observe a random computation error approximately once every 100 lines of code. What is going on here?
The above thought experiment may not be very realistic since current classical computer hardware is extremely reliable. However, the same cannot yet be said of current quantum computers. Quantum computers hold the potential to solve certain computational tasks, such as quantum simulation or integer factorization with an exponential speed-up compared to their classical counterparts.
To outperform classical computers in these tasks, a quantum computer must be able to execute long sequences of highly accurate elementary operations, including single- and two-qubit logic gates, qubit readout, and qubit reset. In state-of-the art superconducting quantum computers, there occur approximately 1-10 errors per every 10 000 single-qubit gates and 10-100 errors per every 10 000 two-qubit gates. These error rates have improved drastically over the years, but they still are too high to outperform classical computers in NISQ applications of practical relevance or to enable quantum error correction with a reasonable overhead in the number of physical qubits.
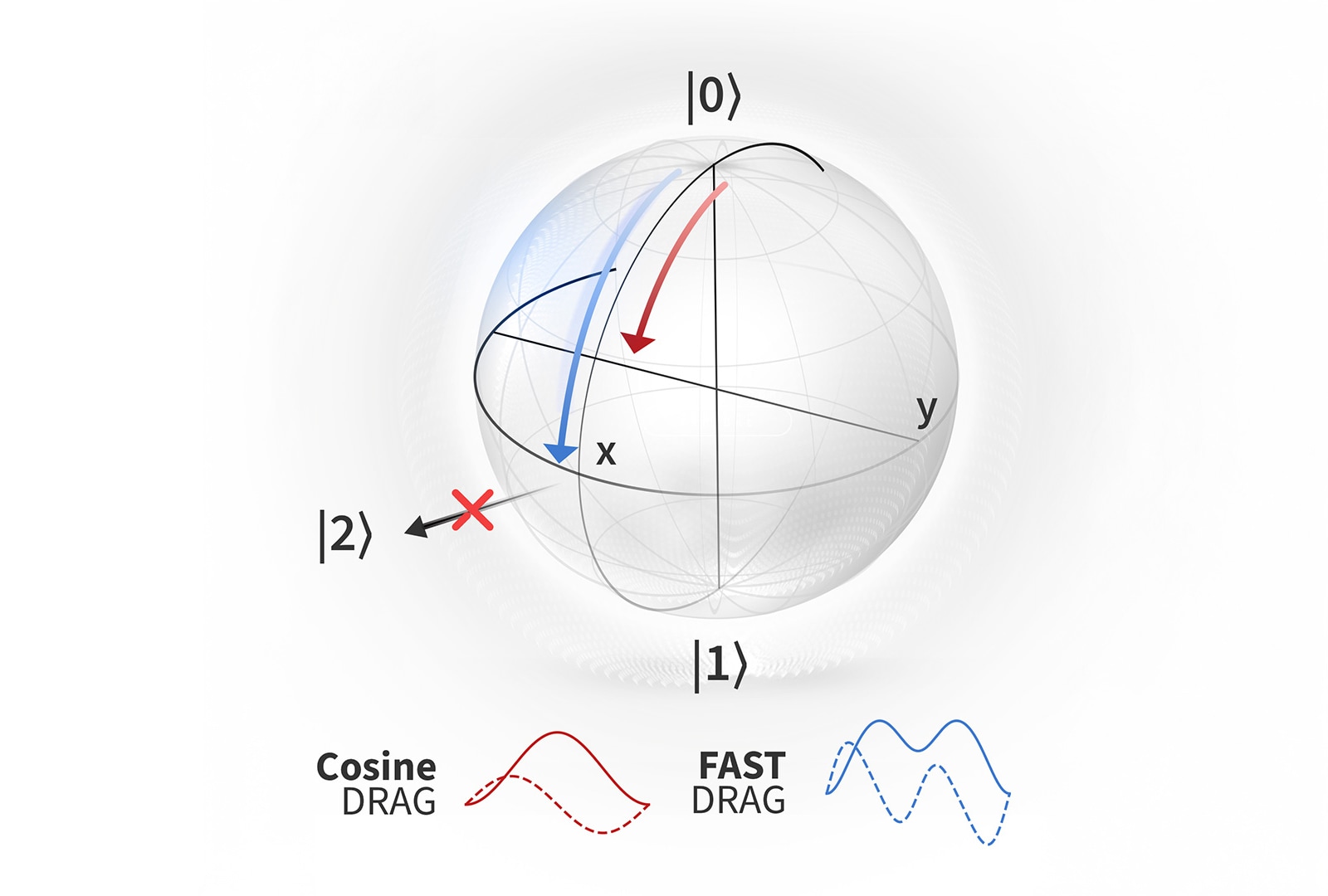
In our new paper, we present novel control methods for reducing the errors of elementary logic operations in superconducting quantum computers, thus enhancing the computational capabilities of present-day quantum computers. We focus on studying single-qubit gates and a specific type of error known as leakage. Leakage limits the speed of elementary logic operations and is particularly harmful for quantum error correction. More precisely, we propose novel control pulse shapes, FAST DRAG and HD DRAG, that enable us to reduce the leakage error of fast single-qubit gates by an order of magnitude compared with previous best methods—even for very short gate durations down to 6 ns.
Trade-off between gate speed and error
Most superconducting quantum computers use transmon qubits to store and process quantum information. A transmon qubit has many discrete energy levels but typically the two lowest-energy levels—denoted by 0 and 1—are used as the qubit states. The higher-excited states—labelled as 2, 3, and so forth—are regarded as non-computational states or leakage states. Single-qubit gates on a transmon qubit are realized with microwave control pulses that are on resonance with the 0-1 transition frequency. Importantly, transmon qubits suffer from a low anharmonicity, meaning that the frequency difference between the 1-2 and 0-1 transitions is only approximately 5%. Due to the low anharmonicity, a single-qubit control pulse targeting the 0-1 transition may accidentally end up exciting the transmon to the second-excited state, thus causing a leakage error.
To estimate the rate of leakage errors, we need to consider the frequency-domain representation of the control pulse, i.e., its Fourier transform and the corresponding spectral energy density. Critically, a high spectral energy density at the 1-2 transition frequency can activate the transition to the second-excited state leading to leakage errors. A basic result from Fourier analysis states that a short pulse in the time domain has a wide bandwidth in the frequency domain.
Thus, the spectral energy density at the 1-2 transition and the rate of leakage errors are increased if the duration of the single-qubit gate pulse is reduced. This phenomenon resembles the overclocking of a classical computer that leads to an increased error rate in the classical processing unit. In quantum computers, the increased leakage errors prevent the use of fast logic gates that would otherwise have several desirable properties, such as reduced sensitivity to decoherence and potential for faster quantum computations.
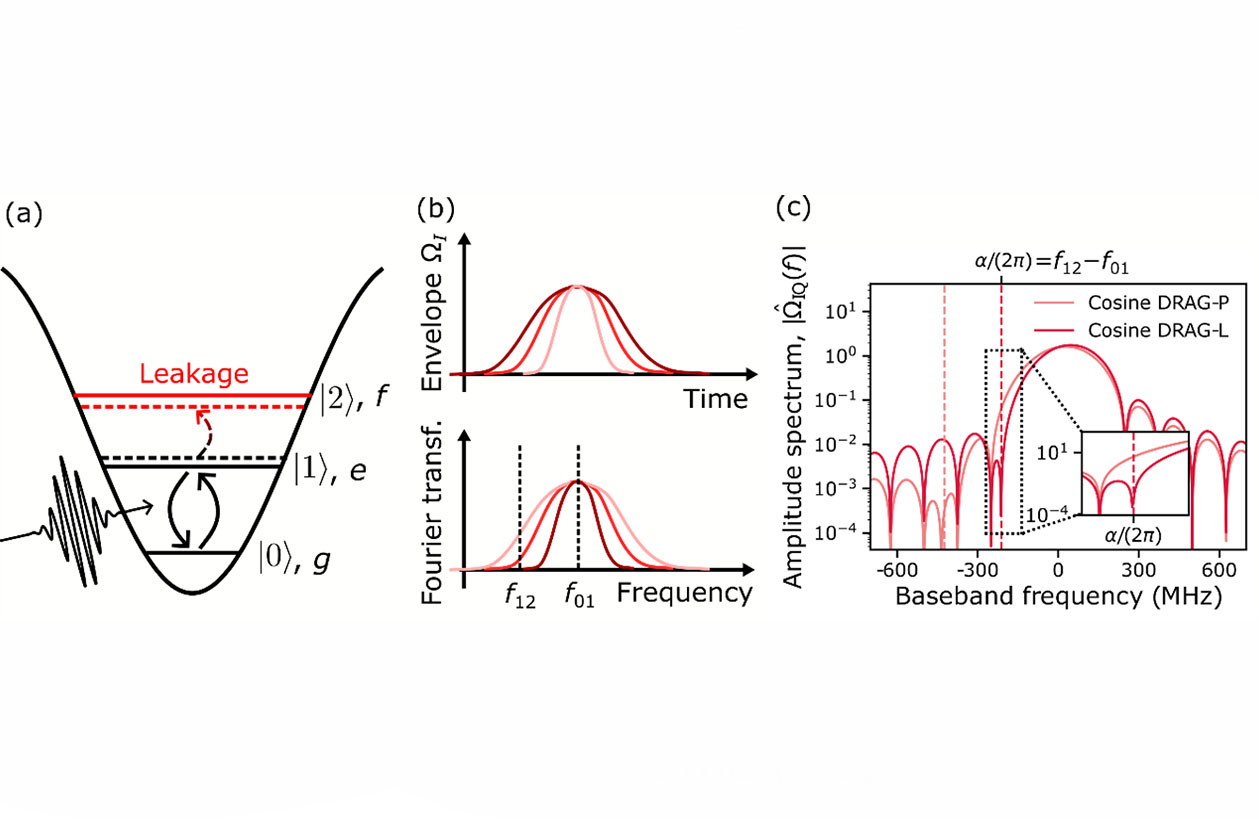
Figure 1. (a) Energy level diagram of a transmon qubit driven with a microwave control pulse. (b) Control pulse envelopes in the time domain and frequency domain. A short pulse (light red) in time domain has a wide bandwidth in the frequency domain. (c) Amplitude spectrum, i.e., absolute Fourier transform for conventional cosine DRAG pulses. A high value of the amplitude spectrum at the anharmonicity α/(2π) leads to an increased leakage error.
Importantly, the probability of leakage errors can be reduced by designing control pulses with a reduced spectral energy density around the 1-2 transition. To date, Derivative Removal by Adiabatic Gate (DRAG) has been the go-to solution for shaping single-qubit control pulses. A microwave control pulse has two independent components known as an in-phase (I) and a quadrature (Q) component. In a conventional DRAG pulse, a cosine envelope or a Gaussian envelope is often used as the in-phase component.
In contrast, the quadrature component is constrained to be proportional to the derivative of the in-phase component. This choice cancels the spectral energy density completely at one frequency. Therefore, the pulse parameters can be calibrated to cancel the spectral energy density at the 1-2 transition frequency, thus reducing leakage errors of fast gates. However, conventional DRAG pulses fail to mitigate leakage if the gate duration is short enough, i.e., 5-10 ns for transmon qubits. This is because the microwave control pulse also slightly changes the 1-2 transition frequency, and therefore, the spectral energy density would need to be reduced across a wider range of frequencies than is possible with conventional DRAG pulses.
Faster gates with lower errors using FAST DRAG
In our paper, we propose two new control pulse shapes, FAST DRAG and HD DRAG, to reduce the leakage errors of single-qubit gates, thus allowing faster gates with lower errors. Both pulse shapes allow the spectral energy density to be strongly reduced across a wider frequency range than is possible with conventional DRAG pulses, which enables lower leakage errors for fast single-qubit gates.
In a FAST DRAG pulse, the in-phase component of the control pulse is expanded as a cosine series, and the coefficients of the cosine series are analytically solved to minimize the spectral energy density across specified frequency ranges, including the 1-2 transition. In HD DRAG, the control pulse is expanded as a sum of a basis envelope and its higher derivatives, and the coefficients of the derivatives are chosen to strongly suppress the spectral energy density at the 1-2 transition.
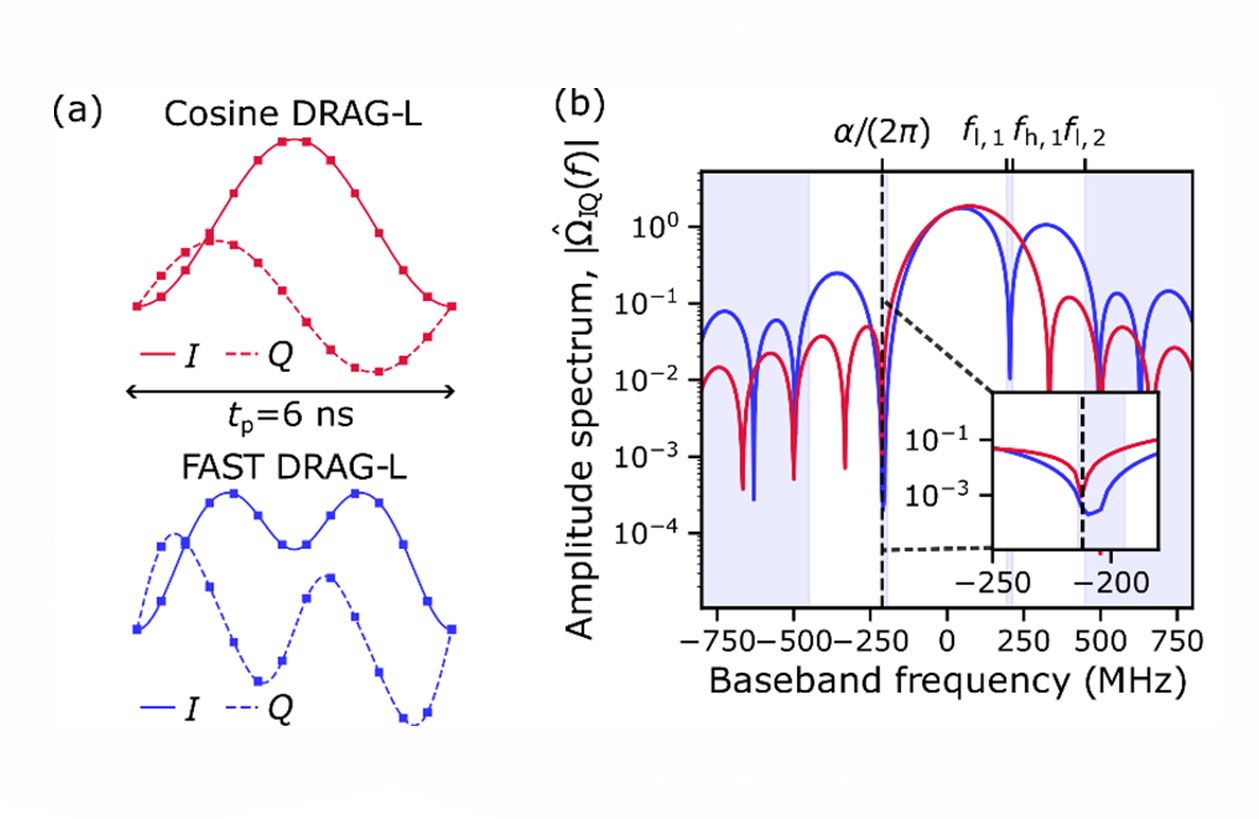
Figure 2. (a) In-phase and quadrature components of a conventional cosine DRAG pulse (red) and the proposed FAST DRAG pulse (blue). (b) Amplitude spectrum of the cosine DRAG and FAST DRAG pulses. As shown in the inset, the FAST DRAG pulse has reduced spectral energy around the 1-2 transition frequency leading to a reduced leakage error.
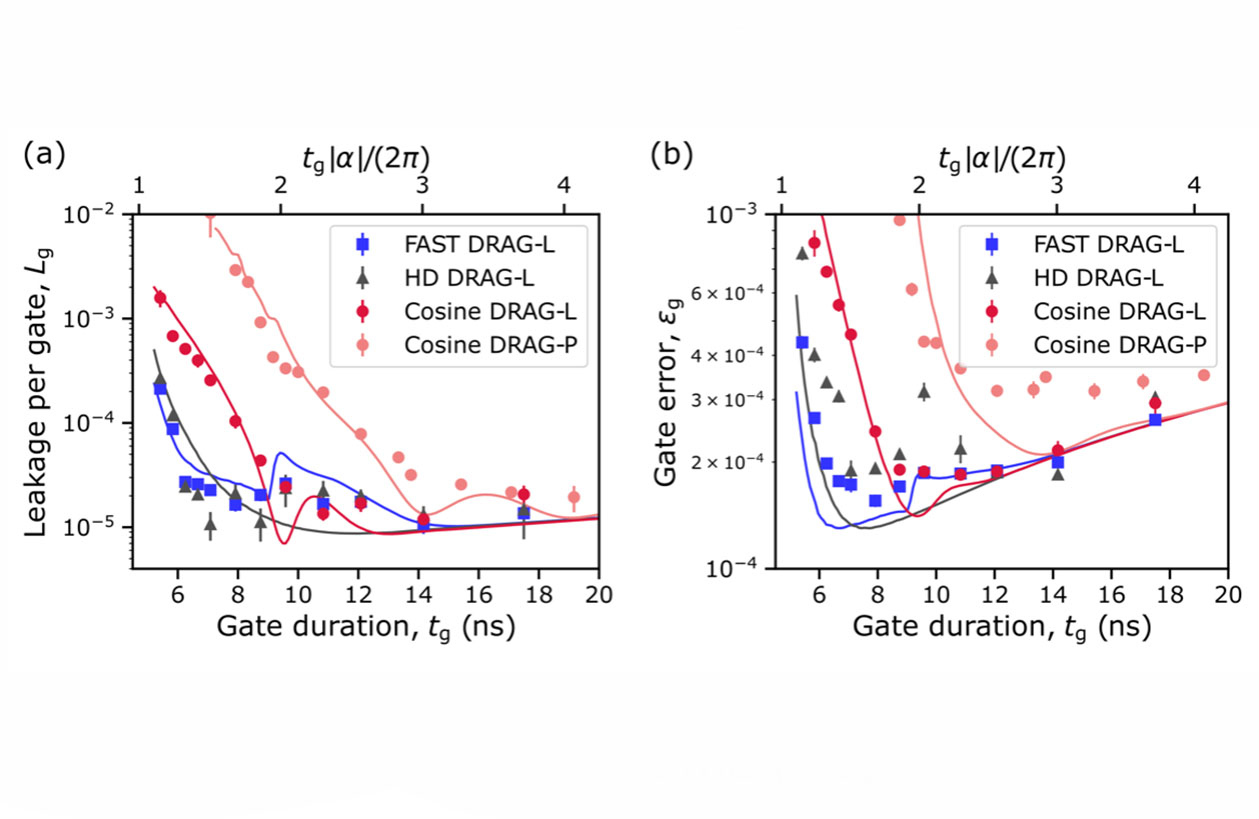
Figure 3. (a) Leakage per single-qubit gate as a function of gate duration for the proposed FAST DRAG and HD DRAG pulses and the conventional cosine DRAG pulses. (b) Single-qubit gate error as a function of gate duration for the same pulses. FAST DRAG allows a faster gate with a lower error than cosine DRAG.
To demonstrate the control pulses in experiments, we study a transmon qubit with an anharmonicity of -212 MHz. Using FAST DRAG pulses, we achieve a low leakage error below 3×10-5 even for single-qubit gate durations as short as 6 ns. For comparison, the conventional cosine DRAG pulse results in a 20-times higher leakage error, and the previous record for comparably fast transmon-based gates is an order of magnitude higher. Furthermore, we show that the FAST DRAG pulse outperforms the conventional cosine DRAG pulse both in terms of the lowest gate error and gate speed. Namely, the FAST DRAG pulse allows us to achieve a gate error of 1.6×10-4 at a gate duration of 7.9 ns, whereas the conventional cosine DRAG pulse reaches its lowest error of 1.8×10-4 at a gate duration of 10.8 ns.
Importantly, the proposed FAST DRAG and HD DRAG pulses enable efficient parameter calibration using simple error-amplification experiments similarly to conventional DRAG pulses. As a further benefit, FAST DRAG and HD DRAG pulses reduce the required peak power of fast single-qubit gates, thus decreasing compression effects and thermal heat load to the cryostat.
Microwave control pulse distortions – an often-overlooked error mechanism
In our quest to optimize the single-qubit gate fidelity, we observe that the total gate error exceeds the sum of incoherent errors and leakage errors. This suggests that there are still coherent errors present. These coherent errors are reduced if we increase the delay between consecutive pulses without changing the gate duration. Such an observation may be explained by distortions of the microwave control pulses that may be caused by, e.g., pulse reflections due to impedance mismatches.
In typical systems, these distortions are much smaller than the distortions of flux pulses that are nowadays routinely pre-compensated for high-fidelity two-qubit gates in flux-based schemes. However, based on our results, we believe that the mitigation of microwave control pulse distortions may also be increasingly needed in the future as the fidelities of single-qubit gates continue to be improved and the gate speeds are pushed further. We classify microwave pulse distortions into intra-quadrature and cross-quadrature distortions. To study the distortions and calibrate pre-compensation parameters, we developed a simple error-amplification experiment to detect coherent errors caused by intra-quadrature distortions. We pre-compensate the control envelopes assuming an exponential distortion model and observe a systematic reduction in the total gate error measured from randomized benchmarking. However, further work is needed to better understand the origin of the distortions, and to develop improved methods for predistortion since our method is limited to the mitigation of intra-quadrature distortions.
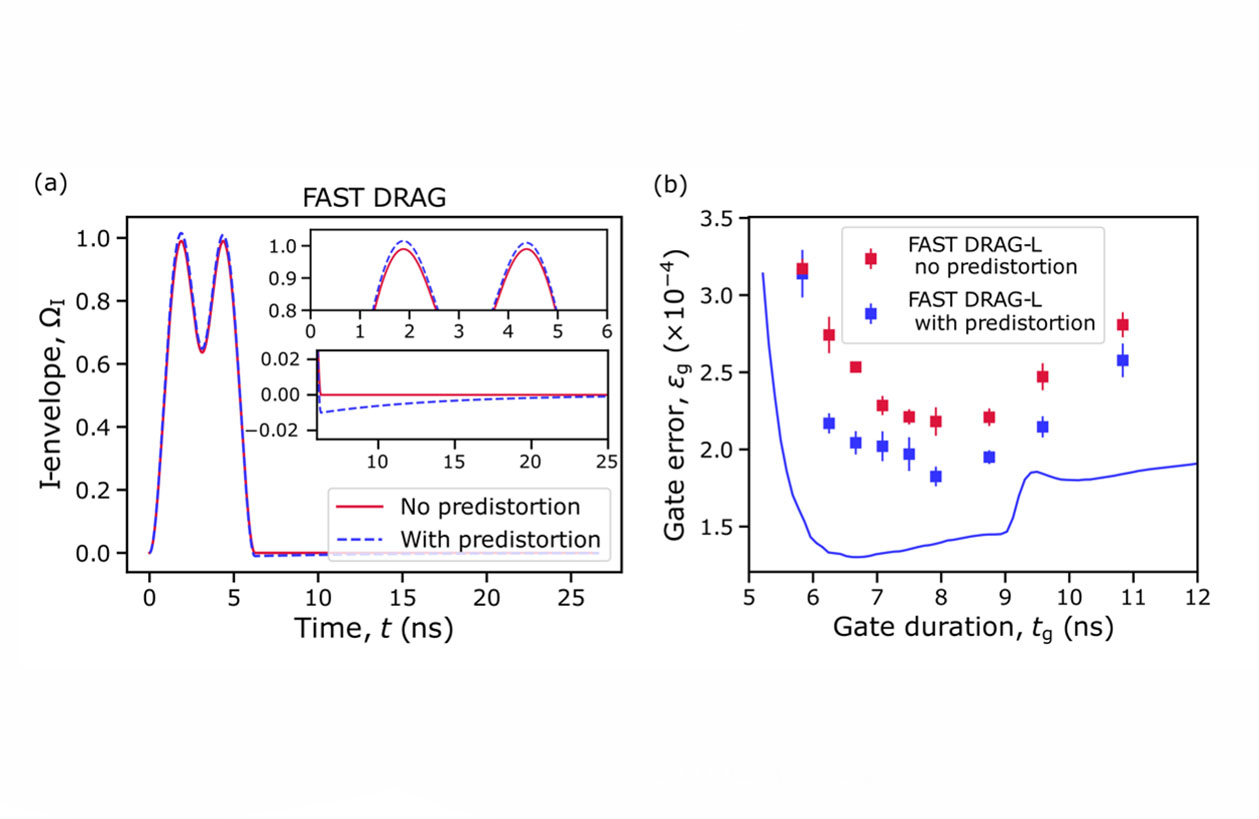
Figure 4. (a) In-phase envelope of a FAST DRAG pulse without predistortion (red) and with predistortion (dashed blue). (b) The predistortion reduces the gate error measured from randomized benchmarking across studied gate durations.
Conclusions
We have developed new control methods to increase the fidelity and speed of single-qubit gates. The proposed control pulse shapes reduce the leakage error of fast single-qubit gates by an order of magnitude compared with previously demonstrated methods. The proposed FAST DRAG approach provides a general framework for shaping control pulses in the presence of undesired transitions and thus, it has the potential to also improve simultaneous single-qubit gates and two-qubit gates in any architecture suffering from leakage transitions.
We also introduce new techniques for the characterization and mitigation of microwave control pulse distortions that may become a major source of single-qubit gate error as fidelities continue to be improved. Overall, our work contributes to the improvement of quantum logic gates, thus enhancing the computational capabilities of current quantum processors.
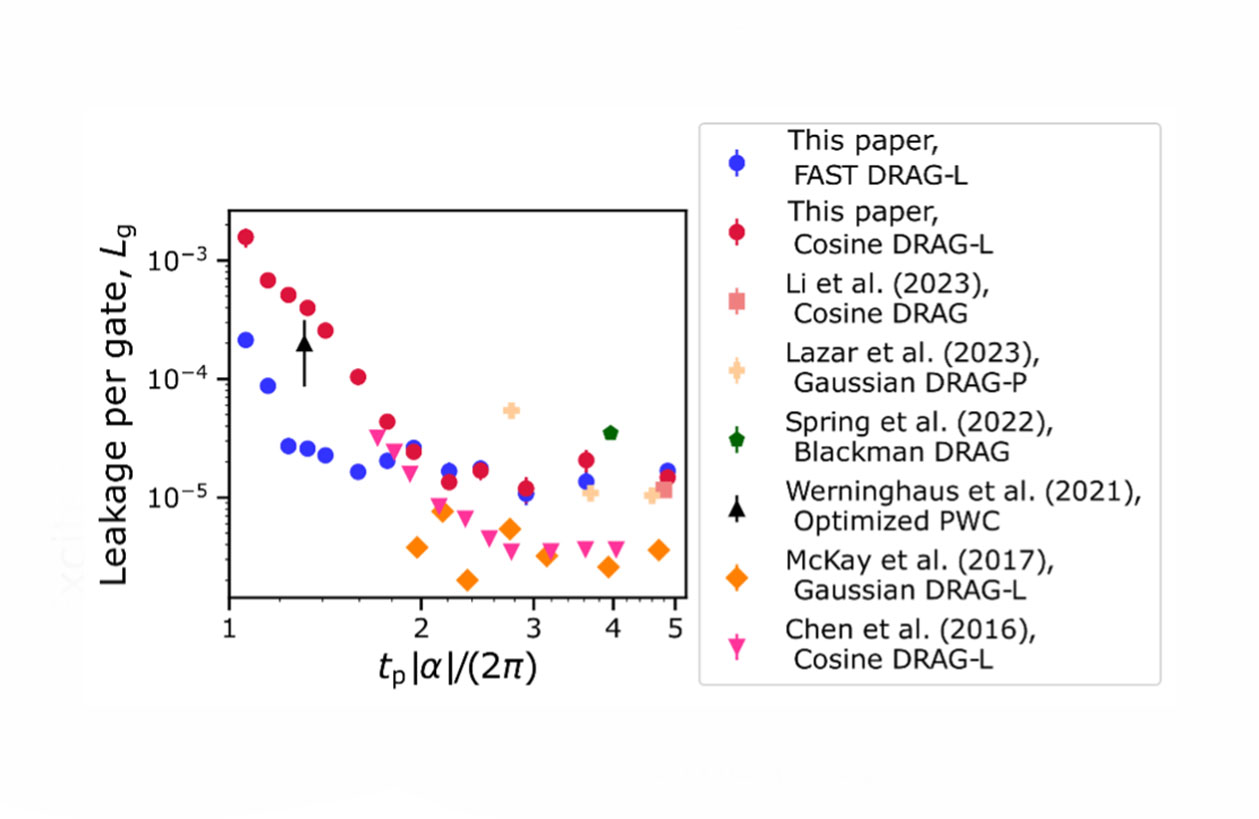
Figure 5. Leakage error as a function of normalized pulse duration for FAST DRAG (blue) and cosine DRAG (red) pulses from our paper together with results from previous single-qubit gate studies on transmon qubits.
Download the paper here:
https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.5.030353

Eric Hyyppä is a quantum engineer at IQM Quantum Computers and a final-year doctoral student at Aalto University. In his research, Eric currently develops improved methodologies for the calibration and benchmarking of quantum logic gates in superconducting quantum computers. Previously, he has also studied novel superconducting qubit types, such as the unimon qubit. Eric also has years of experience in developing algorithms for LiDAR data to enhance and automate forest inventories. In his spare time, he likes to spend time outdoors running, cross-country skiing, and cycling.
Search faster—hit Enter instead of clicking.